Cox’s risk matrix theorem and its implications for project risk management
Introduction
One of the standard ways of characterising risk on projects is to use matrices which categorise risks by impact and probability of occurrence. These matrices provide a qualitative risk ranking in categories such as high, medium and low (or colour: red, yellow and green). Such rankings are often used to prioritise and allocate resources to manage risks. There is a widespread belief that the qualitative ranking provided by matrices reflects an underlying quantitative ranking. In a paper entitled, What’s wrong with risk matrices?, Tony Cox shows that the qualitative risk ranking provided by a risk matrix will agree with the quantitative risk ranking only if the matrix is constructed according to certain general principles. This post is devoted to an exposition of these principles and their consequences.
Since the content of this post may seem overly academic to some of my readers, I think it is worth clarifying why I believe an understanding of Cox’s principles is important for project managers. First, 3×3 and 4×4 risk matrices are widely used in managing project risk. Typically these matrices are constructed in an intuitive (but arbitrary) manner. Cox shows – using very general assumptions – that there is only one sensible colouring scheme (or form) of these matrices. This conclusion was surprising to me, and I think that many readers may also find it so. Second, and possibly more important, is that the arguments presented in the paper show that it is impossible to maintain perfect congruence between qualitative (matrix) and quantitative rankings. As I discuss later, this is essentially due to the impossibility of representing quantitative rankings accurately on a rectangular grid. Developing an understanding of these points will enable project managers to use risk matrices in a more logically sound manner.
Background and preliminaries
Let’s begin with some terminology that’s well known to most project managers:
Probability: This is the likelihood that a risk will occur. It is quantified as a number between 0 (will definitely not occur) and 1 (will definitely occur).
Impact (termed “consequence” in the paper): This is the severity of the risk should it occur. It can also be quantified as a number between 0 (lowest severity) and 1(highest severity).
Note that the above scales for probability and impact are arbitrary – other common choices are percentages or a scale of 0 to 10.
Risk: In many project risk management frameworks, risk is characterised by the formula: Risk = probability x impact. This formula looks reasonable, but is typically specified a priori, without any justification.
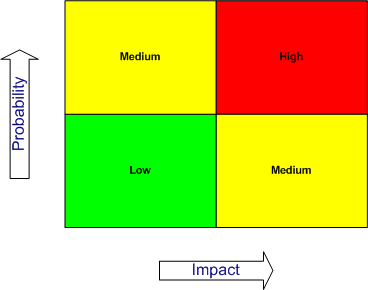
A risk can be plotted on a two dimensional graph depicting impact (on the x-axis) and probability (on the y-axis). This is typically where the problems start: for most risks, neither the probability nor the impact can be accurately quantified. The standard solution is to use a qualitative scale, where instead of numbers one uses descriptive text – for example, the probability, impact and risk can take on one of three values: high, medium and low (as shown in Figure 1 below). In doing this, analysts make the implicit assumption that the categorisation provided by the qualitative assessment ranks the risks in correct quantitative order. Problem is, this isn’t true.
Let’s look at the simple case of two risks A and B ranked on a 2×2 risk matrix shown in Figure 2 below. Let’s assume that the probability and impact of each of the two risks are independent and uniformly distributed between 0 and 1. Clearly, if the two risks have the same qualitative ranking (high, say), there is no way to rank them correctly unless one has quantitative knowledge of probability and impact – which is usually not the case. In the absence of this information, there’s a 50% chance (all other factors being equal) of ranking them correctly – i.e. one is effectively “flipping a coin” to choose which one has the higher (or lower) rank. This situation highlights a shortcoming of risk matrices: poor resolution. It is not possible to rank risks that have the same qualitative ranking.
“That’s obvious,” I hear you say – and you’re right. But there’s more: if one of the ratings is medium and the other one is not (i.e. the other one is high or low), then there is a non-zero chance of making an incorrect ranking because some points in the cell with the higher qualitative rating have a lower quantitative value of risk than some points in the cell with the lower qualitative ranking. Look at that statement again: it implies that risk matrices can incorrectly assign higher qualitative rankings to quantitatively smaller risks – i.e. there is the possibility of making ranking errors. This point is seriously counter-intuitive (to me anyway) and merits a proof, which Cox provides and I discuss below. Before doing so, I should also point out that the discussion of this paragraph assumes that the probabilities and impacts of the two risks are independent and uniformly distributed. Cox also points out that the chance of making the wrong ranking can be even higher if the joint distribution of the two are correlated. In particular, if the correlation is negative (i.e. probability decreases as impact increases), a random ranking is actually better than that provided by the risk matrix. In this situation the information provided by risk matrices is “worse than useless” (a random choice is better!). Negative correlations between probability and impact are actually quite common – many situations involve a mix of high probability-low impact and low probability-high impact risks. See the paper for more on this.
Weak consistency and its implications
With the issues of poor resolution and ranking errors established, Cox asks the question: What can be salvaged? The underlying problem is that the joint distribution of probability and impact is unknown. The standard approach to improving the utility of risk matrices is to attempt to characterise this distribution. This can be done using artificial intelligence tools – and Cox provides references to papers that use some of these techniques to characterise distributions. These techniques typically need plentiful data as they attempt to infer characteristics of the joint distribution from data points. Cox, instead, proposes an approach that is based on general properties of risk matrices – i.e. an approach that prescribes a set of rules that ensure consistency. This has the advantage of being general, and not depending on the availability of data points to characterise the probability distribution.
So what might a consistency criterion look like? Cox suggests that, at the very least, a risk matrix should be able to distinguish reliably between very high and very low risks. He formalises this requirement in his definition of weak consistency, which I quote from the paper:
A risk matrix with more than one “colour” (level of risk priority) for its cells satisfies weak consistency with a quantitative risk interpretation if points in its top risk category (red) represent higher quantitative risks than points in its bottom category (green)
The notion of weak consistency formalises the intuitive expectation that a risk matrix must, at the very least, distinguish between the lowest and highest (quantitative) risks. If it can’t, it is indeed “worse than useless”. Note that weak consistency doesn’t say anything about distinguishing between medium and lowest/highest risks – merely between the lowest and highest.
Having defined weak consistency, Cox derives some of its surprising consequences, which I describe next.
Cox’s First Lemma: If a risk matrix satisfies weak consistency, then no red cell (highest risk category) can share an edge with a green cell (lowest risk category).
Proof: To see how this is plausible, consider the different ways in which a red cell can adjoin a green one. Basically there are only two ways in which this can happen, which I’ve illustrated in Figure 3. Now assume that the quantitative risk of the midpoint of the common edge is a number n (n between 0 and 1). Then if x and y and are the impact and probability, we have
xy=n or y=n/x
So, the locus of all points having the same risk (often called the iso-risk contour) as the midpoint is a rectangular hyperbola with negative slope (i.e. y decreases as x increases). The negative slope (see Figure 3) implies that the points above the iso-risk contour in the green cell have a higher quantitative risk than points below the contour in the red cell. This contradicts weak consistency. Hence – by reductio ad absurdum – it isn’t possible to have a green cell and a red cell with a common edge.
Cox’s Second Lemma: if a risk matrix satisfies weak consistency and has at least two colours (green in lower left and red in upper right, if axes are oriented to depict increasing probability and impact), then no red cell can occur in the bottom row or left column of the matrix.
Proof: Assume it is possible to have a red cell in the bottom row or left column. Now consider an iso-risk contour for a sufficiently small risk (i.e. a contour that passes through the lower left-most green cell). By the properties of rectangular hyperbolas, this contour must pass through all cells in the bottom row and the left-most column, as shown in Figure 4. Thus, by an argument similar to the one of the previous lemma, all points below the iso-risk contour in either of the red cells have a smaller quantitative risk than point above it in the green cell. This violates weak consistency, and hence the assumption is incorrect.
An implication that follows directly from the above lemmas is that any risk matrix that satisfies weak consistency must have at least three colours!
Surprised? I certainly was when I first read this.
Between-ness and its implications
If a risk matrix provides a qualitative representation of the actual qualitative risks, then small changes in the probability or impact should not cause discontinuous jumps in risk categorisation from lowest to highest category without going through the intermediate category. (Recall, from the previous section, that a weakly consistent matrix must have at least three colours).
This expectation is formalised in the axiom of between-ness:
A risk matrix satisfies the axiom of between-ness if every positively sloped line segment that lies in a green cell at its lower end and a red cell at its upper end must pass through at least one intermediate cell (i.e. one that is neither red nor green).
By definition, no 2×2 cell can satisfy between-ness. Further, amongst 3×3 matrices, only one colour scheme satisfies both weak consistency and between-ness. This is the matrix shown in Figure 1: green in the left and bottom columns , red in upper right-most cell and yellow in all other cells. This, to me, is a truly amazing consequence of a couple of simple, intuitive axioms.
Consistent colouring and its implications
The basic idea behind consistent colouring is that risks that have the identical quantitative values should have the same qualitative ratings. This is impossible to achieve in a discrete risk matrix because iso-risk contours cannot coincide with cell boundaries (Why? Because iso-risk contours have negative slopes whereas cell boundaries have zero or infinite slope – i.e. they are horizontal or vertical lines). So, Cox suggests the following: enforce consistent colouring for extreme categories only – red and green – allowing violations for intermediate categories. What this means is that cells that contain iso-risk contours which pass through other red cells (“red contours”) must be red and cells that contain iso-risk contours which pass through other green cells (“green contours”) must be green. Hence the following definition of consistent colouring:
- A cell is red if it contains points with quantitative risks at least as high as those in other red cells, and does not contain points with quantitative risks as small as those on any green cell.
- A cell is green if it contains points with risks at least as small as those in other green cells, and does not contain points with quantitative risks as high as those in any red cell.
- A cell has an intermediate colour only if it a) lies between a red cell and a green cell or b) it contains points with quantitative risks higher than those in some red cells and also points with quantitative risks lower than those in some green cells.
An iso-risk contour is green if it passes through one or more green cells but no red cells and a red contour is one which passes through one or more red cells but no green cells. Consistent colouring then implies that cells with red contours and no green contours are red; and cells with green contours and no red contours are green (and, obviously, cells with contours of both colours are intermediate)
Implications of the three axioms – Cox’s Risk Matrix Theorem
So, after a longish journey, we have three axioms: weak consistency, between-ness and consistent colouring. With that done, Cox rolls out his theorem – which I dub Cox’s Risk Matrix Theorem (not to be confused with Cox’s Theorem from statistics!), which can be stated as follows:
In a risk matrix satisfying weak consistency, between-ness and consistent colouring:
a) All cells in the leftmost column and in the bottom row are green.
b) All cells in the second column from the left and the second row from the bottom are non-red.
The proof is a bit long, so I’ll omit it, making a couple of plausibility arguments instead:
- The lower leftmost cell is green (by definition), and consistent colouring implies that all contours that lie below the one passing through the upper right corner of this cell must also be green because a) they pass through the lower leftmost cell which is green and b) none of the other cells they pass through are red (by Cox’s second lemma). The other cells on the lowest or leftmost edge of the matrix can only be intermediate or green. That they cannot be intermediate is a consequence of between-ness.
- That the second row and second column must be non-red is also easy to see: assume any of these cells to be red. We then have a red cell adjoining a green cell, which violates between-ness.
I’ll leave it at that, referring the interested reader to the paper for a complete proof.
Cox’s theorem has an immediate corollary which is particularly interesting for project managers who use 3×3 and 4×4 risk matrices:
A tricoloured 3×3 or 4×4 matrix that satisfies weak consistency, between-ness and consistent colouring can have only the following (single!) colour scheme:
a) Leftmost column and bottom row coloured green.
b) Top right cell (for 3×3) or four top right cells (for 4×4) coloured red.
c) All other cells coloured yellow.
Proof: Cox’s theorem implies that the leftmost column and bottom row are green. The top right cell must be red (since it is a tricoloured matrix). Consistent colouring implies that the two cells adjoining this cell (in a 4×4 matrix) and the one diagonally adjacent must also be red (this cannot be so for a 3×3 matrix because these cells would adjoin a green cell which violates Cox’s first lemma). All other cells must be yellow by between-ness.
This result is quite amazing. From three very intuitive axioms Cox derives essentially the only possible colouring scheme for 3×3 and 4×4 risk matrices.
Conclusion
This brings me to the end of this post on the Cox’s axiomatic approach to building logically consistent risk matrices. I highly recommend reading the original paper for more. Although it presents some fairly involved arguments, it is very well written. The arguments are presented with clarity and logical surefootedness, and the assumptions underlying each argument are clearly laid out. The three principles (or axioms) proposed are intuitively appealing – even obvious – but their consequences are quite unexpected (witness the unique colouring scheme for 3×3 and 4×4 matrices). Further, the arguments leading up to the lemmas and theorems bring up points that are worth bearing in mind when using risk matrices in practical situations.
In closing I should mention that the paper also discusses some other limitations of risk matrices that flow from these principles: in particular, spurious risk resolution and inappropriate resource allocation based on qualitative risk categorisation. For reasons of space, and the very high likelihood that I’ve already tested my readers’ patience to near (if not beyond) breaking point, I’ll defer a discussion of these to a future post.
Note added on 20 December, 2009:
See this post for a visual representation of the above discussion of Cox’s risk matrix theorem and the comments that follow.





This is good, it is counter intuitive to me. I think there is some problem but I dont know how to express it. Will have to thin about it.
LikeLike
Robert Higgins
July 2, 2009 at 12:01 am
K,
Good paper and discussion of a critical topic.
One critical error though. The calculation of Risk = Probabilty x Impact can not be performed mathematically. The variables Probability and Impact are both probability distributions. The multiplication operator cannot be performed on these.
Many risk literature treat them as scalars. They are PDF’s.
See the DoD PMBOK’s risk section for a better approach. As well see Dr. Edmund Conrow’s Effective Risk Management: Some Keys to Success, 2nd Edition for all the gory details as to why this multiplication approach is not only flawed it is simple wrong.
Also the NASA IRMA, Active Risk Manager (a UK product) on how quantitative assessments of risk are assigned to the 5 rows and 5 columns, to replace the lo, med, hi type attributes.
We use this approach on our manned spaceflight program. For each class of risk – say the propulsion system – the 5 levels of each axis are defined in specific engineering terms. Then the risk management processs convenes the risk board to perform the data gathering for each active risk, puts this into the matrix and produces the risk assessment and the needed risk retirement or mitigation activities that are then found in the master scehdule.
LikeLike
Glen B. Alleman
July 2, 2009 at 3:16 pm
K. This is a really great paper. My calculus and statistics are fuzzy math memories for me now. Probably, doesn’t help that my statistics professor was 1.2 Meters high and she could only write on the bottom 20 cm of the blackboard, and her English was pretty good considering she had only learned it a few years ago.
So I need to just check that I am getting this. K. is basically saying that we can not have a simple 2×2 matrix with a red risk in the lower right corner because the “iso risk contour” has a negative slope. So the green “Low” box has a higher probability than the red “High”.
But Glen is correctly pointing out that the numbers are not simple scalar numbers. For example .7 X .7 = .49. He is saying that they are Probability Density Functions which is basically the area of a section of a bell curve graph. And Calculus prohibits us from using the simple multiplication operation on these complex PDF values?
So using a simple 2 x 2 risk matrix is ok, as long as we don’t try to relate the risk events together? And we recognize it is as mostly a visual communication tool to get people focused on the danger areas?
As we scale up in size and budget especially, on a larger project in which human life is factored in, the model is hopelessly flawed and an “Integrate Risk Management Application” needs to be employed with the Risk Control Board.
Thanks to both of you K and Mr. Allemen for sharing your deep knowledge!
LikeLike
Robert Higgins
July 3, 2009 at 12:01 am
Robert,
Thanks for your comments.
Glen is absolutely correct – probability and impact are distributions, not scalars. The conclusions of the paper apply to analyses in which risk is defined by an analytic formula (such as probability x impact). Such an approach is commonly used because the joint distribution of probability and impact is hard to determine in practice. For programs such as the ones Glen refers to – manned spaceflight – the effort involved in doing it right is justifiable; in other cases a “quick and dirty” analytical approach may be more suitable. Cox’s work shows that in the latter case, certain consistency rules follow from the axioms (or assumptions) of weak consistency, between-ness and consistent colouring.
Regards,
Kailash.
LikeLike
K
July 3, 2009 at 6:01 am
Glen
Thanks for your insightful comment. I agree – strictly speaking, probability and impact should both be treated as random variables, and as probability theory tells us,the joint distribution of two random variables equals the product of their individual distributions only if the two variables are independent (which isn’t true in most cases).
Now, ideally, one would like to know the joint distribution of probability and impact. Unfortunately this this is often hard to determine in practice, and appears to be an active area of research. As Cox mentions in the paper, “…Several directions for advancing research on risk matrices appear promising. One is to consider applications in which there are sufficient data to draw some inferences about the statistical distribution of (Probability, Consequence) pairs. If data are sufficiently plentiful, then statistical and artificial intelligence tools such as classification trees, rough sets, and vector quantization can potentially be applied to help design risk matrices that give efficient or optimal (according to various criteria) discrete approximations to the quantitative distribution of risks…”
However, notwithstanding the above, one can start with an a priori definition of risk as probability x impact (or any other analytical formula). Cox’s lemmas and theorem apply to such analyses which, though lacking in rigour, are quite commonly used. The paper demonstrates (convincingly?) that certain rules must be followed in order to maintain consistency, even when simplistic analyses are employed.
Regards,
Kailash.
LikeLike
K
July 2, 2009 at 7:11 pm
Kailash,
This is an important thread of discussion in many ways. As well there is a wealth of literature on the use and application of risk matrices that does not follow the approaches of the paper, but are used in high risk domains – manned space flight and nuclear power are two examples I’m familiar with.
I’m not sure NASA and US DoD share Cox’s approach about the analytical aspects of the risk matrix as pairs. Cox’s approach is certainly common outside that domain. PMBOK uses this. But DoD PMBOK removes the calculation. PMBOK 4th edition moves away entirely from the use of calculation and toward the NASA/DoD approach is predefining the Impact scales and using the probability of occurrence to select with cell of the 5×5 to look at for the color.
The result is that a Risk Value (the old probability x impact) is abandoned in place of a “risk buy down” plan held in the Integrated Master Schedule through some external. The figures shown in Table V., would not be found in NASA and the nuclear domain, because the numeric value of impacts are replaced by narrative descriptions of the actual operational impacts from the occurrence of the risk. These narratives are developed through analysis of the system.
So the underlying quantitative model mentioned on §3 of the paper has only one side that is probabilistic – the probability of occurrence. The impacts are defined through the Risk Management process. This is also the approach used in US Department of Energy Nuclear Safety and Safeguards. Again the quantitative risk as a product is abandoned in place of a classification of response to a predefined consequence.
Just as an observation the Lemma §3.2 may not have actual applicability in the field. The Lemma is based on the continuous transition of risk exposure. There are situations where binary failure modes exist so the risk is either Green or Red with no recovery state. Propulsion systems and nuclear weapons materials handling have this mode. Either “we’re OK,” or “we’re dead.” In the US we use the phrase “there is no such thing as a ‘little’ leakage from a nuclear power plant.” Three Mile Island set that notion in our minds. For example “allowable outage time (AOT)” risk models have Red and Green touching for dual train nuclear generating units.
LikeLiked by 1 person
Glen B. Alleman
July 3, 2009 at 1:01 am
Glen,
Thanks so much for your very interesting comments and insights into how risk is analysed in high risk domains.
The approach of using narrative descriptions of impact is a logically sound one as it sidesteps all the mathematical inconsistencies that Cox highlights.
You’re also right that all of Cox’s arguments tacitly assume that the risk function is continuous. The conclusions do not apply if risk is described by a discrete function (such as we’re OK/ we’re dead).
Regards,
Kailash.
LikeLike
K
July 3, 2009 at 6:18 am
K,
In the current NASA Systems Engineering Handbook SP-2007-6105, Chapter 6.4 has a nice overview of how the matrix can be used without doing the calculation and speaks to the limitations of the Risk Matrix.
education.ksc.nasa.gov/…/NASA%20SP-2007-6105%20Rev%201%20Final%2031Dec2007.pdf
I have some other “examples” of the classification of the consequences that drive the use of the matrix if your interested.
LikeLike
Glen B. Alleman
July 4, 2009 at 2:52 am
Glen,
This has been a very useful discussion. To sum up: simplistic analyses, wherein risk is characterised using continuous analytic functions, are often invalid for the reasons you mention in your comments. Even in the situations that they are applicable, Cox’s analysis shows that inconsistencies result from representing risk rankings on a rectangular grid. Unfortunately such analyses are quite commonly promoted by project management texts and courses.
Thanks again for your comments and references.
Regards,
Kailash.
LikeLike
K
July 6, 2009 at 6:21 pm
Hi Kailash,
Great post and excellent comments from Glen. But you’ve still left the question of correlating correct quantitative values to the correct qualitative scales open. Will that be really possible? Even if one were to go by Glen’s comments of discrete values will it be accurate?
LikeLike
Prakash
July 10, 2009 at 3:12 pm
Prakash,
That’s a good question. Let’s look at continuous risk functions first. For this case, Cox shows that a correlation between qualitative categories (as described in rectangular risk matrices) and quantitative values of risk (as described by a risk function) isn’t possible. Typically one will have inconsistencies at qualitative region boundaries – between high and medium, say – regardless of the shape of the function. Why? Because in general iso-risk contours will not coincide with grid boundaries.
In the discrete case it is easier to ensure consistency because one can design the grid so as to avoid intersections of boundaries with data points. This is also a more logical way to look at risk. As Glen points out in his comment above – risk events are often discrete, not continuous (as in his we’re OK / we’re dead example).
Regards,
Kailash.
LikeLike
K
July 11, 2009 at 9:40 am
[…] couple of months ago I wrote an article highlighting some of the pitfalls of using risk matrices. Risk matrices are an example of scoring methods , techniques which use ordinal scales to assess […]
LikeLike
On the limitations of scoring methods for risk analysis « Eight to Late
October 6, 2009 at 4:27 pm
Thanks to all for the discussion, especially to K and Glenn. However, considering I got to this site while looking for examples where IBIS is used to capture discussions, I kept wondering “Could the essence of the discussion be represented more efficiently or clearer if IBIS was used instead of text?”
If so, would someone volunteer?
Please?
Thanks again to the contributors.
[Observers may note that not using IBIS opens an area of discussion, not necessarily regarding the limitations of IBIS. Reasons may include social issues. Perhaps this line of inquiry has already been addressed.]
LikeLike
Tony Waisanen
December 15, 2009 at 2:16 am
Tony,
Thanks for an excellent idea. I’ll have a go at it…
Regards,
K.
LikeLike
K
December 15, 2009 at 8:32 am
[…] a comment » Some time ago I wrote a post on a paper by Tony Cox which describes some flaws in risk matrices (as they are commonly used) and […]
LikeLike
Visualising content and context using issue maps – an example based on a discussion of Cox’s risk matrix theorem « Eight to Late
December 18, 2009 at 11:16 pm
Tony (and others),
An IBIS map of the post and discussion has been published here.
Comments/suggestions for improvement are welcomed!
Regards,
Kailash.
LikeLike
K
December 19, 2009 at 7:40 am
[…] matrices) is “worse than useless.” See my posts on the limitations of scoring techniques and Cox’s risk matrix theorem for detailed discussions of these […]
LikeLike
The failure of risk management: a book review « Eight to Late
February 11, 2010 at 10:12 pm
Kalish,
In your article, section titled “Between-ness and its implications” you state:
“…only one colour scheme satisfies both weak consistency and between-ness. This is the matrix shown in Figure 1: green in the lower left-most cell, red in upper right-most cell and yellow in all other cells.”
Yet Figure 1 shows green in the entire left-most column and along the entire bottom row. Based on my read of the rest of the article (especially “Implications of the three axioms…” section) I think this is the proper coloring, therefore the quoted statement in the Between-ness section must be wrong.
Comment?
LikeLike
Jeff Gray
July 1, 2010 at 5:42 am
Jeff,
You are absolutely right: between-ness and weak consistency imply that the only legitimate 3×3 matrix is one which is coloured green in the left and bottom columns, red in the upper right cell and yellow elsewhere. I have now fixed this in the post.
Thanks so much for pointing this out – I really appreciate it.
Regards,
Kailash.
LikeLike
K
July 1, 2010 at 6:18 am
[…] on sound methodologies. Unfortunately, ad-hoc techniques abound in risk analysis: see my posts on Cox’s risk matrix theorem and limitations of risk scoring methods for more on these. Risk metrics based on such techniques […]
LikeLike
Six common pitfalls in project risk analysis « Eight to Late
June 3, 2011 at 4:00 pm
[…] Cox’s risk matrix theorem and its implications for project risk management: Describes some logical flaws in the way risk matrices are commonly used. Based on: Cox, L. A., What’s wrong with risk matrices?, Risk Analysis, Volume 28, pages 497-512 (2008) […]
LikeLike
From here to serendipity: gaining insights from project management research « Eight to Late
July 5, 2011 at 6:23 am
K
This is an excellent post and very interesting series of comments. I was hoping you might be able to clarify a query I have regarding 5×5 matrices.
My organisation uses a 5×5 matrix with four colours that seems to violate Cox’s Lemmas on several fronts. However, rather than having probabability and severity scales ranging from 0-1 as per the examples in Cox’s paper, we have probabability and severity scales ranging from 1-5 resulting in a maximum score of 25.
In addition, rather than being presented as “corresponding to numerical intervals” (i.e. [0,1], [1,2] etc) the categories on each axis and resulting scores are presented as corresponding to whole numbers i.e.
5 5 10 15 20 25
4 4 8 12 16 20
3 3 6 9 12 15
2 2 4 6 8 10
1 1 2 3 4 5
1 2 3 4 5
Each of these scores then has one of four colours superimposed on it.
Am I right in concluding that a) this 5×5 matrix can only have 3 colours, and b) that the colour scheme must follow one of the two patterns shown in table V of Cox’s paper?
Many thanks in advance.
-Mark
[0, 0.2), [0.2, 0.4), [04, 0.6), [0.6, 0.8), and [0.8,
1],
LikeLike
Mark
September 9, 2011 at 8:40 pm
Hi Mark,
Thanks for your comment and interest.
The key assumption in Cox’ s argument is that the underlying risk function is continuous. If this isn’t so, then weak consistency and between-ness do not apply. As Glen Alleman has mentioned in his comment: many real-life risk functions are discrete, not continuous. However, there are situations in which a continuous function is more appropriate. Cox gives an example of a situation in the paper, and I quote:
“The discrete qualitative categories provided in guidance such as Table VIII are also inconsistent with the continuous quantitative nature of many physical hazards. For example, should a condition that causes
“negligible” environmental damage on each occurrence (e.g., leaking 1 ounce of jet fuel per occurrence) but that causes a high frequency of these small events (e.g., averaging 5 events per hour) truly have a lower severity rating than a second condition that causes more damage per occurrence (e.g., leaking 10 pounds of jet fuel per occurrence) but that causes less frequent occurrences (e.g., once per week)?” (see pg. 509)
So the question is: is your underlying risk function discrete or continuous? The applicability of Cox’s analysis depends on the answer.
Hope this helps.
Regards,
Kailash.
LikeLike
K
September 11, 2011 at 7:12 am
Interestingly I find that there are 8 iso-contours in a 5×5 matrix that comply with Cox’x axioms/lemmas. Is this right?
LikeLike
Gavin Lawrence
December 30, 2011 at 12:16 am
Hi Gavin,
My apologies for the delay in responding to you. I’ve been on leave so have been somewhat tardy with correspondence.
First up, thanks so much for the shout out on LinkedIn. My post has got a great deal of attention over the last week or so as a result of your links to it.
Regarding your question, I reckon there will be a large number of contours that satisfy Cox’s theorem for 5×5 matrices. Here’s why:
Consider the two 5×5 matrices described by Cox on page 505 of the paper. Both matrices have a red cell in the top right corner. Now, any iso-risk contour that lies wholly in this cell is consistent with Cox’s axioms. As an example contours that are of the form x*y=n where n is any number that lies in the interval (0.9,0.92) will lie wholly in this cell and will therefore satisfy the axioms. From the denseness property of real numbers, there are an infinite number of distinct points in the interval (0.9,0.92) and hence an infinite number of possible contours. QED.
(Note: I could have picked any other interval that lies wholly in [0.8,1] – (0.92,0.95), for example).
Thanks again for your interest in my article and the links to it- I truly appreciate it!
Regards,
Kailash.
LikeLike
K
January 8, 2012 at 12:46 am
I am not sure that this is the correct interpretation.
I can send my analysis in a word doc for you to pplay with if you let me know your email address and you can add it to your site.
LikeLike
Gavin Lawrence
January 8, 2012 at 5:35 am
Hi Gavin,
I would love to see your analysis as it is quite possible that I have misinterpreted the term. I’ve sent you an email message.
Regards,
Kailash.
LikeLike
K
January 8, 2012 at 11:02 am
I have to say that Cox’s paper is extremely difficult to come to grips with. I have had a couple of post-grad interns trying to wrestle with it and convert it into a practical comprehensible set of matrix construction instructions – a sort of car workshop manual but they didn’t get very far..
Hubbard makes extensive references to but I don’t think it is really going to be the answer to life the universe and everything.
Hubbard talks extensively of x-axis value compression but makes no reference to log scaling. Cox multiplies impact by probability but if both scales were log you would add them, but what if P() is cardinal and value is log – mulitply or add?
LikeLike
glawrence768
January 8, 2012 at 8:10 pm
Gavin,
Thanks for the thought provoking comment.
You may have hit upon a problem that is not uncommon at the interface between theory and practice. Theoretical models are often based on idealised assumptions that ignore some of the messiness and complexity of real life situations . As a result it can be difficult, if not impossible, to apply theoretical models to real life problems. I suspect (but am not certain) that this is the case here.
I think there is a great deal of truth in the notion of risk as a social construct. I have discussed this in relation to IT project risks in this post.
Cox is referring to the situation in which both scales are linear. Log-log or log-linear plots do not change the underlying relationship, which is still multiplicative. Cox’s arguments would still apply as one could, in principle, choose to display the plot on linear-linear axes (though the display may be hard to read!). As before, I’m not sure I’ve interpreted your comment correctly, so feel free to straighten me out if I haven’t.
Regards,
Kailash.
LikeLike
K
January 10, 2012 at 10:42 pm
Reblogged this on Machinery Safety 101 and commented:
This is an excellent article discussing some of the issues around one of the most common risk assessment tools: The Scoring Matrix.
LikeLike
Doug Nix
February 7, 2012 at 6:31 am
Outstanding to all. I enjoyed the collective effort to solution resolution to life’s daily events “risk probability outcome and impact consequences” but then comes;
“VoR” – Velocity of Risk …. food for thought …. http://www.mccormickpcs.com/rm/vor.html
Predicting the future is still a guessing game and mathematics will always give us our comfort zone but reality is that variables are infinite therefore predicting probability will always be a crap shoot. You all know that managing risk is only achievable by those variables that we can control and even then we’re still risk factoring probability which is simply “mitigating risk probability” (making less severe).
Risk simply put is – “Yes”, “No”, “Maybe”. Yes can be “we’re OK and No can be “we’re dead” and maybe is “it’s not life threatening”. We all mitigate risk every moment of our lives – “walking across the street” every event is different with varying degrees of “risk”; the road is wet/dry, many cars or few, wearing safe shoes or not…. all the variables analyzed in seconds and probability factor concluded and decision made – to run or not run! Outcome can be good or bad, alive, dead or just a few broken bones “risk impact”.
The human factor is the highest risk contributor, for logic (common since) is too often side stepped and the 33,808 US driving fatalities in 2009 due to excessive speeding is the result of the “human factor”.
Risk is just a bunch of molecules bouncing around with an infinite probability of impact and the end result is the inevitable outcome when it happens.
“To boldly go where no man has gone before” is what makes us human and that’s why we take risk.
Take care to all.
LikeLike
Mike McCormick
February 9, 2012 at 2:42 am
Love your articles. https://www.proggio.com/blog/project-manager-skills-improvisation/
LikeLike
kyleadanza
November 14, 2018 at 11:42 am
Thank you kyleadanza!
LikeLike
K
November 14, 2018 at 11:53 am
[…] Cox’s risk matrix theorem and its implications for project risk management. Introduction One of the standard ways of characterising risk on projects is to use matrices which categorise risks by impact and probability of occurrence. These matrices provide a qualitative risk ranking in categories such as high, medium and low (or colour: red, yellow and green). Such rankings are often used to prioritise and allocate resources to manage risks. […]
LikeLike
Risk | Pearltrees
December 16, 2018 at 2:18 am
[…] la probabilidad de que algo suceda y el impacto comercial (negativo) que tendría. Entonces, si lo ilustramos en una matriz, podremos distinguir zonas según el riesgo, donde los extremos […]
LikeLike
Risk-Based Testing: La Matriz de Riesgos de pruebas de Software | Abstracta Chile
July 19, 2022 at 5:49 am